카페검색 본문
카페글 본문
-
오일러가 없었다면 현대수학은?(현대수학의 개척자 오일러의 신앙) 2023.01.29해당카페글 미리보기
역학에 있어서의 오일러-라그랑주의 방정식, 무한급수에 있어서의 오일러의 변환, 오일러의 정수, 오일러 증명, 오일러 적분, 오일러의 수, 강체 운동에 있어서의 오일러의 각, 오일러의 방정식, 오일러의 공식, 오일러의 동차함수의 정리, 탄성이론에...
-
오일러의 공식 증명...대학수학 2007.12.13해당카페글 미리보기
처음 증명하였다. 지금과 같은 모양의 오일러의 공식은 1748년 오일러가 무한급수의 좌우극한값이 같음을 증명하면서 발표되었다. 그러나 로저와 오일러 모두 이 공식이 지닌 '복소수를 복소평면 위의 하나의 점으로 볼 수 있다'는 기하학적 의미를 눈치...
-
무지 급해여!!!꼭 알려주세여~~~오일러의 공식 증명!!! 2004.10.17해당카페글 미리보기
두시간후의 수학시간에 내야되는데... 아직 못찾구 헤매구만 있어여... 오늘 처음 가입했는데 빨리 좀 답해주세여...!!! 증말 급합니다!!! 오일러 공식 증명이요!!!
-
오일러의 공식에 대해서.. 2014.04.11해당카페글 미리보기
물리의 대가가 따로 설명을 붙일 만큼 수학∙공학∙물리학 등에 중요한 공식이다. 그렇다면 오일러 공식은 어떻게 증명할까? 미분이나, 멱급수 이론 등을 쓰면 오일러 공식을 쉽게 증명할 수 있고, 수많은 교재와 웹사이트에서는 그렇게 설명하고 있다...
-
오일러의 공식(Euler's Identity) e^(iπ)+1=0 해설(증명) 2007.09.16해당카페글 미리보기
역시나 『박사가 사랑한 수식』에 나오는, 오일러의 공식(Euler's Identity)입니다. 이 오일러의 공식 e^(iπ)+1=0 은, 오일러의 공식(Euler's Formula) e^(iθ) = cosθ + i sinθ 에서 유도된 특별한 경우라 할 수 있는데요. 한번 증명해 보겠습니다...
-
세상에서 가장 아름다운 수학 공식! ‘오일러 항등식’ 2022.07.28해당카페글 미리보기
출판된 자신의 책 ‘Introductio in analysin infinitorum’에서 오일러는 처음으로 아름다운 공식인 오일러 항등식을 소개했다. 오일러 항등식의 기반이 되는 오일러 공식을 증명하는 방법은 여러가지가 있다. 테일러 전개, 미분, 적분 등 방법은 다양...
-
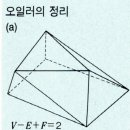
다면체의 구성요소들 사이의 공식, 오일러의 정리 2013.05.03해당카페글 미리보기
다면체는 V-E+F=2(1-p)이다. 이 경우는 위상수학에서 좀 더 자세히 배울 수 있다. 오일러의 정리에 의해 정다면체는 모두 다섯 종류라는 것이 증명되었다. 추가적으로 오일러의 정리에 관한 링크 걸어드립니다. http://blog.naver.com/seokj0801/40041840256
-
이번엔, 오일러 공식 - 기하학적 증명... 부탁드립니다. 2002.03.29해당카페글 미리보기
이라던가...? r이 허근이 나올경우에 오일러의 공식이 쓰이는데, 오일러 공식의 증명법을 알고싶습니다. e^ix = cosx + isinx...안들어 오구요... 복소평면을 이용해서 기하학적으로 증명할수 있다고 들었거든요. 그림그리기 힘드니깐, 혹시 관련 사이트...
-
해당카페글 미리보기
-
Re:오일러 공식이랑 테일러 전개 증명좀 해주세여~ 2002.09.16해당카페글 미리보기
밑에글에아마추어수학자님이쓰시글을한번찾아보세여 --------------------- [원본 메세지] --------------------- 오일러 공식이랑 테일러 전개를 유도 증명 해야하거든여.. 빨리 답변좀 올려 주세여~