카페검색 본문
카페글 본문
정확도순
-
QRM Eliminator 와 Fourier(푸리에) 수학 2023.10.20해당카페글 미리보기
합으로 어떤 것이든 만들 수 있지 않을까? 라는 것이었는데 이 원리를 수학 공식으로 만들어 입증 하였습니다. 그는 푸리에 급수, 푸리에 변환 이론을 만들어 수학공식으로 완성 하였습니다. 오늘날 무선 통신기가 컴퓨터에 의해 수학계산으로 가능해진...
-
푸리에 변환의 유도과정에 대해 질문드립니다. 2023.10.19해당카페글 미리보기
11절은 책의 표현과 많이 다른 것 같아 아래 블로그를 주로 참고했습니다. https://kwon-jjing.tistory.com/m/32 1. 먼저 푸리에 급수에서, 공학수학에서의 일반적인 설명은 경계값을 반주기의 +-로 놓고 시작하는 것으로 이해했습니다. 기본서에서는 0...
-
# 교류 해석을 위한 푸리에 정리 2023.04.18해당카페글 미리보기
조합으로 나타낼 수 있다. 이 절에서는 푸리에 정리의 개념과 어떻게 정현파 신호를 해석하는지 살펴본다. 이때 삼각 푸리에 급수의 상수와 계수의 값에 대한 해석을 통해 정현파 신호의 중요성을 이해하고자 한다. # 처음 만나는 회로이론, 방성완, p.189
-
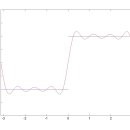
Re:사각파의 푸리에 급수 전개. 2005.02.09해당카페글 미리보기
Leibniz 가 1673년 경에 기하학적 고찰로부터 얻은 것이라고 하네요. 한편 이 결과는 유명한 푸리에 급수전개로부터도 얻을 수 있습니다. 푸리에 급수 전개라는 것은 임의의 주기성을 가지는 함수를 sin 과 cos 의 무수한 합에 의해 표현 가능하다는 이론...
-
푸리에 급수, Fourier Series 2009.08.12해당카페글 미리보기
푸리에 급수, Fourier Series 1. 개요 o 주기함수의 시간영역 신호를 서로 직교하는 삼각함수 또는 지수함수의 합으로 표현함 o 푸리에 급수의 계수를 이용하여 진폭과 위상에 대한 선 스펙트럼을 그릴 수 있음 2. 표현 방법 가. 삼각함수형 표현 나. 지수...